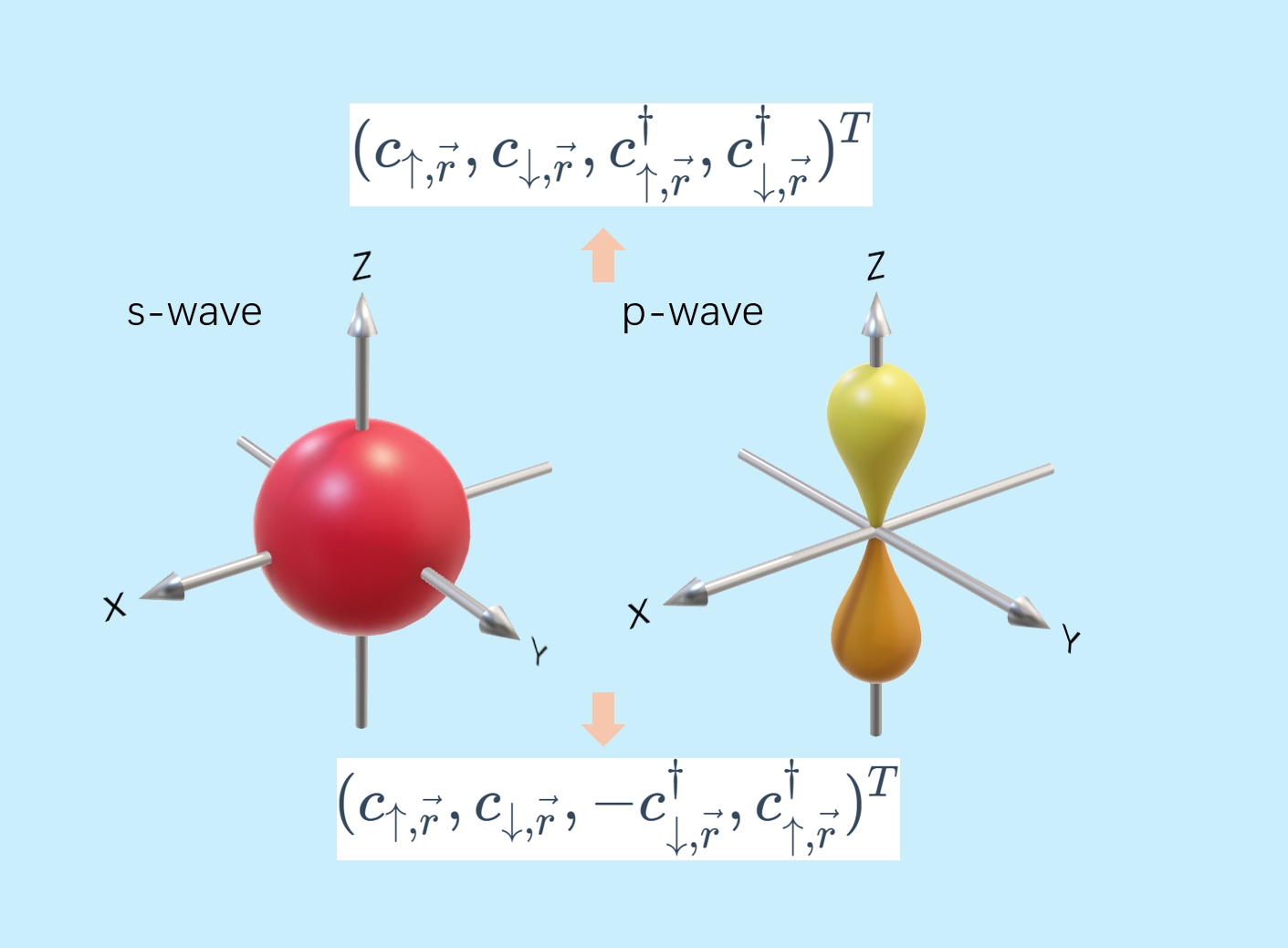
BdG Equation in tight-binding approximation

X.-Z. CHEN, 17/05/2024, EIT, Ningbo

BdG Hamiltonian

Let us consider a two-dimensional electron system with Rashba spin-orbit-coupling (SOC)¹, Dresselhaus SOC², spatialy-varying magnetic texture and proximity-induced superconductivity. The time-independent Schrodinger
describing such an electron is written in real space as

$\begin{pmatrix} H_0 & i\Delta(\vec{k}) \sigma_y \\ -i \Delta(\vec{k}) \sigma_y & -H_0^{*} \\ \end{pmatrix}\begin{pmatrix} \psi_e\\ \psi_h\\ \end{pmatrix} =E\begin{pmatrix} \psi_e\\ \psi_h\\ \end{pmatrix}$

where $\psi_e=[c_{\uparrow,\vec{r}},c_{\downarrow,\vec{r}}]^{T},\psi_h=[c_{\uparrow,\vec{r}}^{\dagger},c_{\downarrow,\vec{r}}^{\dagger}]^{T}$ is the wavefunction in Nambu spaces, $\Delta$ is the superconductor order parameter, $E$ are the energy eigenvalues and

$H_0 = \left( \frac{\vec{p}^2}{2m}-\mu \right)\sigma_0 -\frac{\alpha}{\hbar}(p_x\sigma_y-p_y\sigma_x)+ \frac{\gamma}{\hbar} p_x\sigma_z + \vec{J}(\vec{r}) \cdot \vec{\sigma}$

where $\vec{J}(\vec{r}) \cdot \vec{\sigma}=J_x\sigma_x + J_y\sigma_y + J_z\sigma_z$,
$\vec{p}=(p_x,p_y,p_z)$ are the momentum operators, with $p_{i}=-i\hbar\partial_{i}$ ($i=x,y,z$), $m$ is the effective mass of electron, $\mu$ is the chemical potential, $\alpha$ is the strength of Rashba SOC, $\gamma$ is the strength of Dresselhaus SOC, $\vec{J}(\vec{r})$ describes the effective exchange field at position $\vec{r}$, $\vec{\sigma}=(\sigma_x,\sigma_y,\sigma_z)$ are the Pauli
spin matricies, and $\sigma_0$ is the $2\times 2$ unit matrix.

$H_0^{*} = \left( \frac{\vec{p}^2}{2m}-\mu \right)\sigma_0 -\frac{\alpha}{\hbar}(p_x\sigma_y+p_y\sigma_x)- \frac{\gamma}{\hbar} p_x\sigma_z + J_x\sigma_x - J_y\sigma_y + J_z\sigma_z$

so we get

$\begin{split} H_{BdG} &= \left( \frac{\vec{p}^2}{2m}-\mu \right)\tau_z -\frac{\alpha}{\hbar}p_x\tau_z\sigma_y+\frac{\alpha}{\hbar}p_y\sigma_x + \frac{\gamma}{\hbar} p_x\sigma_z \\ & + J_x\tau_z\sigma_x + J_y\sigma_y + J_z\tau_z\sigma_z + \Delta(\vec{r}) \tau_y\sigma_y, \\ \end{split}$

¹. The Rashba effect, also called Bychkov–Rashba effect, is a momentum-dependent splitting of spin bands in bulk crystal and low-dimensional condensed matter systems (such as heterostructures and surface states) similar to the splitting of particles and anti-particles in the Dirac Hamiltonian. Remarkably, this effect can drive a wide variety of novel physical phenomena, especially operating electron spins by electric fields, even when it is a small correction to the band structure of the two-dimensional metallic state. An example of a physical phenomenon that can be explained by Rashba model is the anisotropic magnetoresistance (AMR). Read more ↩

². The Dresselhaus effect is a phenomenon in solid-state physics in which spin–orbit interaction causes energy bands to split. It is usually present in crystal systems lacking inversion symmetry. Read more ↩

Tight-binding approximation

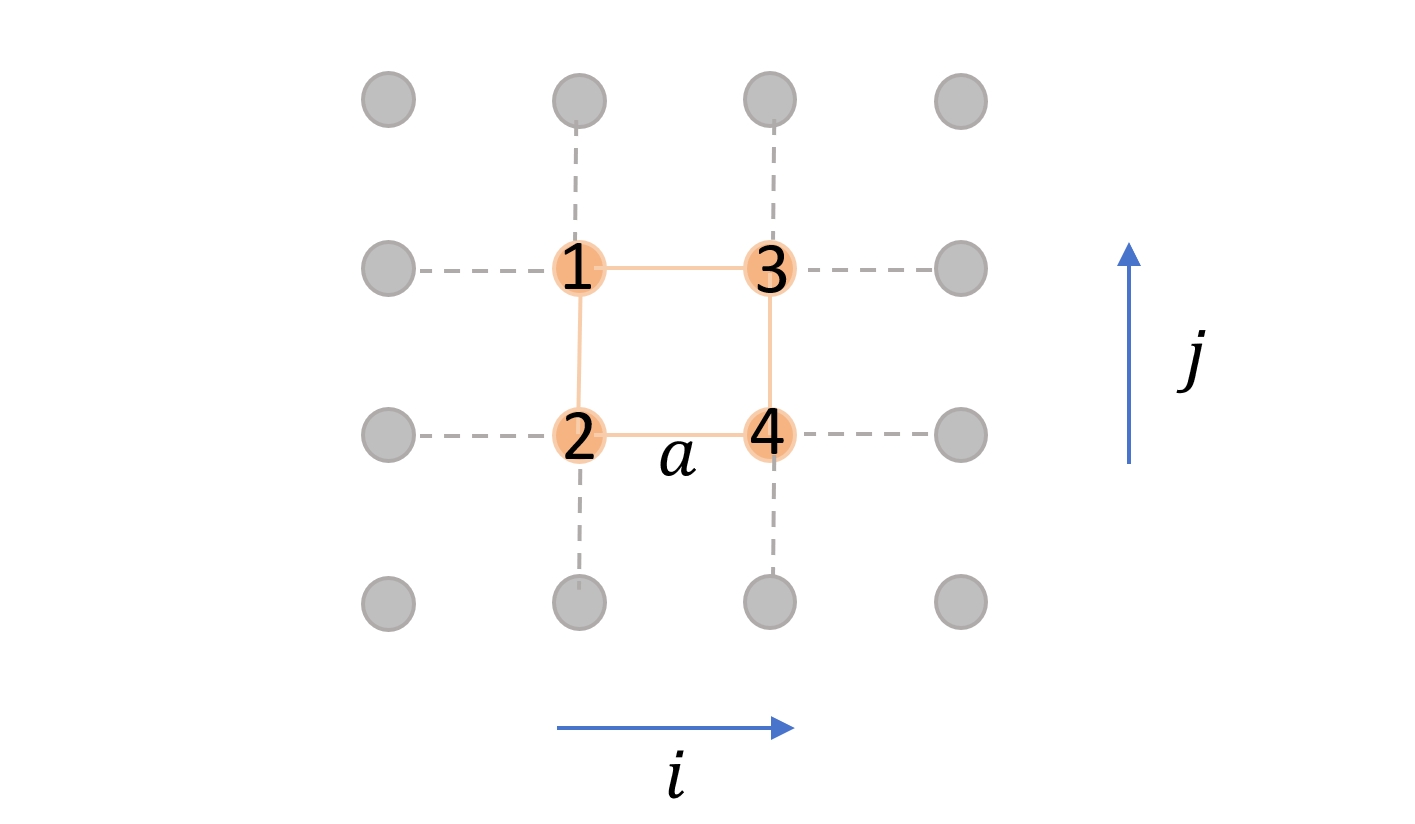
To approximate this Hamiltonian with a discrete model, the momentum operators can be written using finite-difference method. The system is considered as a discrete lattice with the position of a lattice (grid) point given by $\vec{r}=(x,y)=(ai,aj)$, for a square lattice, where a is the unit lattice spacing and $i,j$ are the lattice indices along $x$ and $y$ directions respectively.

Lattice in two-dimensional

Kinetic energy

$\begin{split} \frac{\vec{p}^2}{2m} \psi_{e,h}(x,y) &= -\frac{\hbar^2}{2m} \left[ \frac{\partial^2}{\partial^2 x} + \frac{\partial^2}{\partial^2 y} \right] \psi_{e,h}(x,y)\\ &=-\frac{\hbar^2}{2m} \left[ \frac{\psi_{e,h}(x+a,y)-2\psi_{e,h}(x,y)+\psi_{e,h}(x-a,y)}{a^2} + \mathcal{O}(\Delta x=a)^2 \right]\\ &-\frac{\hbar^2}{2m} \left[ \frac{\psi_{e,h}(x,y+a) - 2\psi_{e,h}(x,y) + \psi_{e,h}(x,y-a)}{a^2} + \mathcal{O}(\Delta x=a)^2 \right] \end{split} \tag{6}$

Using central difference approximation, the higher order terms in the above expression are neglected. The energy is given by

$\begin{split} E_K &= \langle \psi_{e,h}^{\dagger}(x,y) | \frac{p^2}{2m} | \psi_{e,h}(x,y) \rangle \\ &= -\frac{\hbar^2}{2ma^2}(\langle \psi_{e,h}^{\dagger}(x,y)|\psi_{e,h}(x+a,y) \rangle + \langle \psi_{e,h}^{\dagger}(x,y)|\psi_{e,h}(x-a,y)\rangle\\ &\quad +\langle \psi_{e,h}^{\dagger}(x,y) | \psi_{e,h}(x,y+a)\rangle + \langle \psi_{e,h}^{\dagger}(x,y) | \psi_{e,h}(x,y-a) \rangle \\ &\quad -4\langle \psi_{e,h}^{\dagger}(x,y)|\psi_{e,h}(x,y)\rangle) \end{split} \tag{7}$

The above Hamiltonian can be written in terms of the fermionic field operators using second-quantization notation as follows

$H_K = -t \sum_{\langle ij\rangle,\sigma} [c_{i\sigma}^{\dagger}c_{j\sigma}+H.c.] + 4t \sum_{i,\sigma} c_{i\sigma}^{\dagger}c_{i\sigma} \tag{8}$

where $i,j$ are lattices indices, $\langle \rangle$ represents nearest-neighbor lattice sites, $t=\hbar^2/(2ma^2)$ is the nearest-neighbor hopping amplitude and $\sigma=(\uparrow,\downarrow)$ is the spin index.

Rashba SOC

The Hamiltonian, describing Rashba SOC in two-dimensional metallic system, is given by

$H_R = \frac{\alpha}{\hbar} (\sigma_x p_y - \sigma_y p_x) \tag{9}$

Where $\alpha$ is the strength of the SOC. When we operate this Hamiltonian on the wave-function $\psi(x,y)$ at lattice point $(x,y)$, we obtain

$\begin{split} H_R \psi(x,y) &= \frac{\alpha}{\hbar} \left[ \sigma_x \left( -i\hbar\frac{\partial}{\partial y} \right) -\sigma_y \left( -i\hbar \frac{\partial}{\partial x} \right) \right] \psi(x,y)\\ &= -i\alpha \left[ \sigma_x \frac{\partial}{\partial y} -\sigma_y \frac{\partial}{\partial x} \right] \psi(x,y)\\ &=-i\alpha \left[ \sigma_x \frac{\psi(x,y+a)-\psi(x,y-a)}{2a} - \sigma_y\frac{\psi(x+a,y)-\psi(x-a,y)}{2a} \right] \end{split} \tag{10}$

where $a$ is the lattice spacing. The Rashba Hamiltonian can be written in second-quantization notation as

$\begin{split} H_R &= -\frac{i\alpha}{2a} \sum_{\langle ij \rangle} [ c_{i,j,\uparrow}^{\dagger} c_{i,j+1,\downarrow} - c_{i,j,\uparrow}^{\dagger}c_{i,j-1,\downarrow} + i (c_{i,j,\uparrow}^{\dagger}c_{i+1,j,\downarrow}-c_{i,j,\uparrow}^{\dagger}c_{i-1,j,\downarrow})\\ &\quad + c_{i,j,\downarrow}^{\dagger}c_{i,j+1,\uparrow} - c_{i,j,\downarrow}^{\dagger}c_{i,j-1,\uparrow} - i (c_{i,j,\downarrow}c_{i+1,j,\uparrow} - c_{i,j,\downarrow}^{\dagger}c_{i-1,j,\uparrow})] \end{split} \tag{11}$

Zeeman exchange coupling

The effect of the magnetic fringing field enters through a Zeeman exchange coupling term

$H_Z = \vec{J}(\vec{r})\cdot \vec{\sigma} = \frac{1}{2}g\mu_B \vec{B}(\vec{r})\cdot \vec{\sigma} \tag{12}$

where $g$ is the $g$-factor of electrons and $\mu_B$ is Boltzmann constant. In second-quantized notation, $H_Z$ is written as

$H_Z = \frac{1}{2}g\mu_B \sum_{\langle i \rangle} \left[ (B_{xi}-iB_{yi})c_{i,\uparrow}^{\dagger}c_{i,\downarrow} + (B_{xi}+iB_{yi})c_{i,\downarrow}^{\dagger}c_{i,\uparrow} + B_{zi}(c_{i,\uparrow}^{\dagger}c_{i,\uparrow}-c_{i,\downarrow}^{\dagger}c_{i,\downarrow}) \right] \tag{13}$

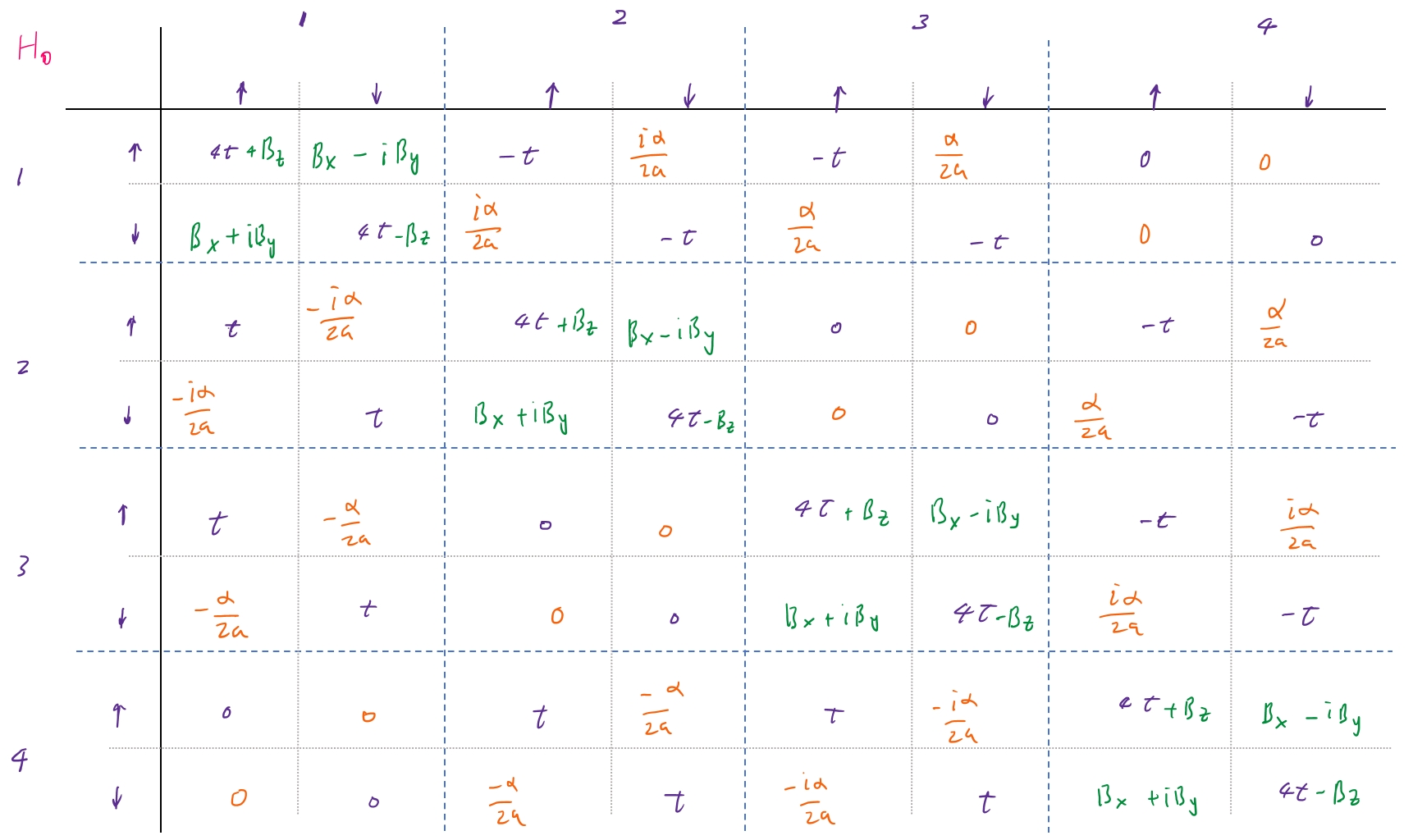
$H_0$ in Tight-binding approximation

Pairing Hamiltonian

The onsite $s$-wave pairing term is written as

$H_S = \sum_{i} \left[ \Delta c_{i,\uparrow}^{\dagger}c_{i,\downarrow}^{\dagger} + \Delta c_{i,\downarrow}c_{i,\uparrow} \right] \tag{14}$

we can apply the transformation between particle and hole (in $k$-space, a Fourier transform) Max Hays-book Eq. (6.6)

$\Delta c_{k,\uparrow}^{\dagger} c_{-k,\downarrow}^{\dagger} + \Delta c_{-k,\downarrow}c_{k,\uparrow} = \Delta c_{k}^{\dagger}h_{k} + \Delta h_{k}^{\dagger}c_{k}$

$H_S$ in Tight-binding approximation